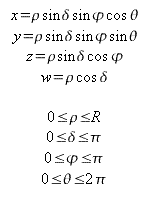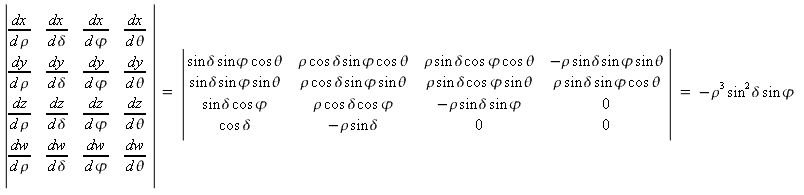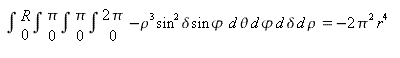Alex,

I'm having a problem with curvilinear coordinates in 4-space. I'm trying to
extend spherical coordinates into 4-space. I can find the determinant of the
Jacobian matrix in 3-space with spherical coordinates, and I can integrate to
get the correct volume. When I try the same thing in 4-space I'm not getting
the right volume, though. I'm trying to add a w coordinate and delta angle the
same way we added phi to extend from polar to spherical coordinates:

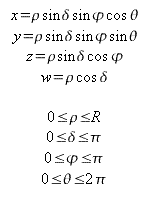
I then calculate the Jacobian matrix and its determinant:

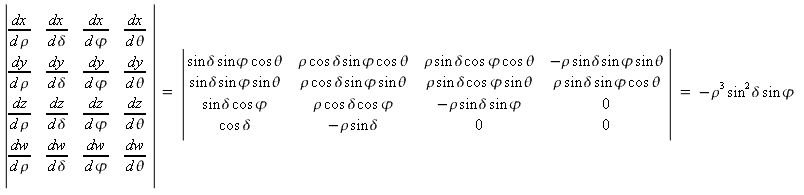
I've done this both by hand and by calculator, multiple times, I'm pretty sure
I've done the calculations correctly. However, when I try to integrate to find
the volume of the 4-sphere, I get the wrong answer:

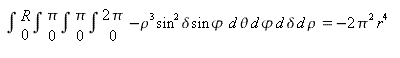
This is obviously wrong; you can't have a negative volume here. Doing the
integral in rectangular coordinates (derived from the rectangular definition of
a n-sphere, not from this), I get 1/2*pi^2*r^4. This also fits the general
formula for the n-volume of the n-sphere I found for the extra credit.

Do you have any idea what I'm doing wrong here?

Thank you,
Morgan LaMoore