Objectives: Determine relationship between linear velocity, centripetal force and acceleration.
Equipment: stopwatch, Fc setup, mass set
Circular Motion
Objectives: Determine relationship between linear
velocity, centripetal force and acceleration.
Equipment: stopwatch, Fc setup, mass set
Methods:
1.
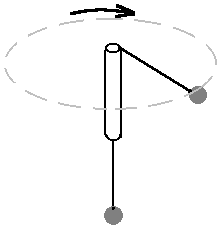
Sketch the Fc setup.
Label the radius, Fc, mass m, reference washer,
mass holder.
2.
Measure the radius with the reference washer at its
desired position. Hang
a 50.0 g mass on the Fc set up.
This mass represents a force Fc = mv2/r.
Let g = 10m/s2 such that a 50.0 g mass has a
weight Fc equal to 0.5 N.
3. Put your goggles
on now. Whirl and
time the stopper for 10 revs in a horizontal circle.
Be sure the reference washer does not move up and
down, and does not touch the handle.
4. Determine the
period T (time) for one revolution, then calculate v, and
ac. The
radius remains constant in this lab.
v = 2πr/T
and ac
= v2/r.
5. Repeat for
various masses to get 4-5 trials (up to a maximum of 250 g).
Analysis:
1.
Plot graphs of:
(a)
Fc vs
ac (ac on the x-axis)
(b)
v2 vs ac
(ac on the x-axis)
2.
Describe the relationship for each graph.
Calculate the slopes for each.
What do the slopes of each graph represent? (Hint: look at
the units for Δy/Δx, then examine your data.)
3.
Describe how adjustments in the radius r would affect the mass=s
velocity given the same Fc.
radius
0.85 m;
C
= 2 π r,
T
= time/revs,
v
=
2πr / T
Let g = 10 m/s2
|
mass
kg |
Fc
(N) |
revs |
time
(s) |
T
(s) |
v
(m/s) |
v2
(m2/s2) |
ac
(m/s2) |
|
0.050 |
|
|
7.2 |
0.72s |
|
|
|
Back to the Brockport High School Science Department